Task space vector handling¶
The output of a task map is a representation of the robot’s state in the task space. Most task spaces are \(\mathbb{R}^n\). As such, they can be stored and handled as vectors of real numbers. However, some task maps output configurations in the \(SO(3)\) or the \(SE(3)\) space. In this case, Lie group algebra has to be used to correctly compute the additions and subtractions in the task space. The task space vector implements operations on task spaces. The task space vector is a data structure that keeps track of \(SO(3)\) sub-groups within the stored vector. The operations on this vector then implement the Lie group algebra. For example, a spatial frame may be stored as a transformation matrix \(M_A^B\in\mathbb{R}^{4\times4}\). This matrix will be stored in the task space vector. Performing addition and subtraction on the vector will then be incorrect. The correct transformation is performed by a matrix multiplication. The task space vector keeps track of transformations stored within its structure and applies the correct operations on them. Furthermore, the result of subtraction is always a geometric twist, e.g., \(M_A^B-M_C^B={^B\boldsymbol{t}_A^C}\). This makes it possible to multiply the result of this operation with a geometric Jacobian, producing a geometrically correct relative transformation. This feature has been used in the implementation of the inverse kinematics solver and the AICO solver. Additionally,
a \(SO(3)\) rotation can be represented and stored in different ways, e.g. as a unit quaternion \(\boldsymbol{R}_\mathcal{Q}\in\mathbb{R}^4 \text{ where } ||\boldsymbol{R}_\mathcal{Q}||=1\), Euler angles \(\boldsymbol{R}_\mathcal{ZYZ},\boldsymbol{R}_\mathcal{ZYX},\boldsymbol{R}_\mathcal{RPY}\in\mathbb{R}^3\), angle-axis representation \(\boldsymbol{R}_\mathcal{A}\in\mathbb{R}^3 \text{ where } ||R_\mathcal{A}||=\theta\), rotation matrix \(\boldsymbol{R}\in\mathbb{R}^{3\times3}\), etc. We handle these representations implicitly. Each sub-group of the task space vector stores the size and type of representation that was used. The operations on the vector first convert the task space coordinates into a rotation matrix representation, then the correct spatial operation is applied and a twist is computed. As a result the input and output dimension may vary, i.e. subtraction of two rotations represented as rotation matrices is a function \(f(R_1, R_2): \mathbb{R}^9 \rightarrow \mathbb{R}^3\). The result is the angular velocity component of the twist. The task space vector is composed by concatenating outputs of multiple task maps. Each task map specifies if its output contains any components that have to be handled using the Lie group algebra.
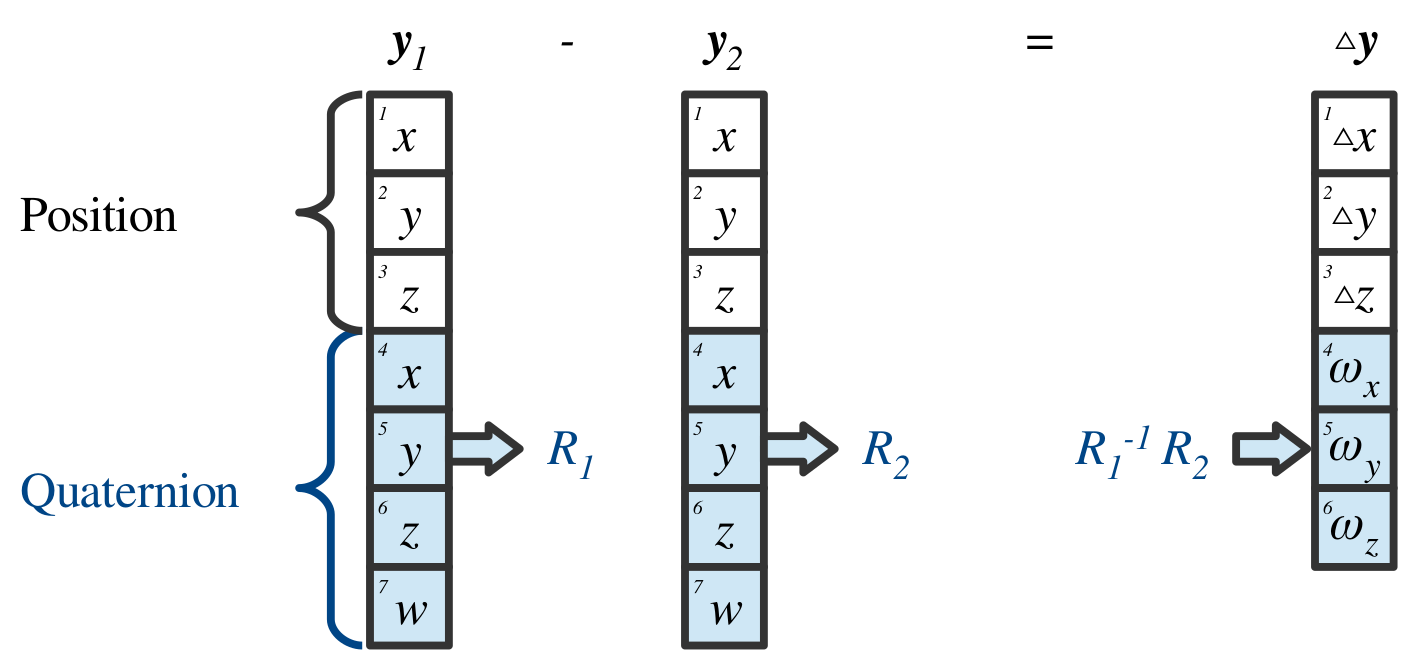
Task space vector data packing combining three position coordinates \(x, y, z\in \mathbb{R}\) and a sub-vector containing a \(SO(3)\) rotation represented as a unit quaternion. The subtraction calculation of two task space vectors \(\boldsymbol{y}_1\) and \(\boldsymbol{y}_2\) first converts the quaternions into rotation matrices \(R_1\) and \(R_2\) and performs the rotation operation \(R_2^{-1}R_1\). The result is then converted into angular velocities \(\omega_x, \omega_y, \omega_z\) and packed into the output vector \(\vartriangle\!\!y\). Notice that the dimensionality of \(\vartriangle\!\!\boldsymbol{y}\in\mathbb{R}^6\) and \(\boldsymbol{y}_1, \boldsymbol{y}_2\in\mathbb{R}^7\) are different.